Streamlit Apps for the topic
05 Applied Hydrogeology
Aquifer Testing
Theis, Neuman, and Hantush Jacob parameter estimation
Fitting formation parameter to REAL measured data
This variant of the app allows to choose real measured data
This interactive document allows to apply the Theis and Neuman principle for pumping test evaluation in unconfined, leaky, and confined transient setups. The notebook is based on an Spreadsheet from Prof. Rudolf Liedl.
General situation
We consider a aquifer with constant transmissivity. If a well is pumping water out of the aquifer, radial flow towards the well is induced. To calculate the hydraulic situation, the following simplified flow equation can be used. This equation accounts for 1D radial transient flow towards a fully penetrating well within a confined aquifer without further sinks and sources:
\[\frac{\partial^2 h}{\partial r^2} + \frac{1}{r} \frac{\partial h}{\partial r} = \frac{S}{T} \frac{\partial h}{\partial t}\]Mathematical model and solution
Theis solution for confined aquifers
Charles V. Theis presented a solution for this by deriving
\[s(r, t) = \frac{Q}{4 \pi T} W(u)\]with the well function
\[W(u) = \int_u^{+\infty} \frac{e^{-\tilde{u}}}{\tilde{u}} d\tilde{u}\]and the dimensionless variable
\[u = \frac{S r^2}{4 T t}\]Neuman solution for unconfined aquifers
ToDo: Provide explanation and theory here
This equations are not easy to solve. Historically, values for the well function were provided by tables or as so called type-curve. The type-curve matching with experimental data for pumping test analysis can be considered as one of the basic hydrogeological methods. However, modern computer provide an easier and more convinient way to solve the 1D radial flow equation based on the Theis approach. Subsequently, the Theis equation is solved with Python routines. The results for the measured data are graphically presented in an interactive plot.

You can access the app here: https://theis-neuman-hantush.streamlit.app/
Theis parameter estimation and drawdown prediction
Fitting formation parameter to REAL measured data
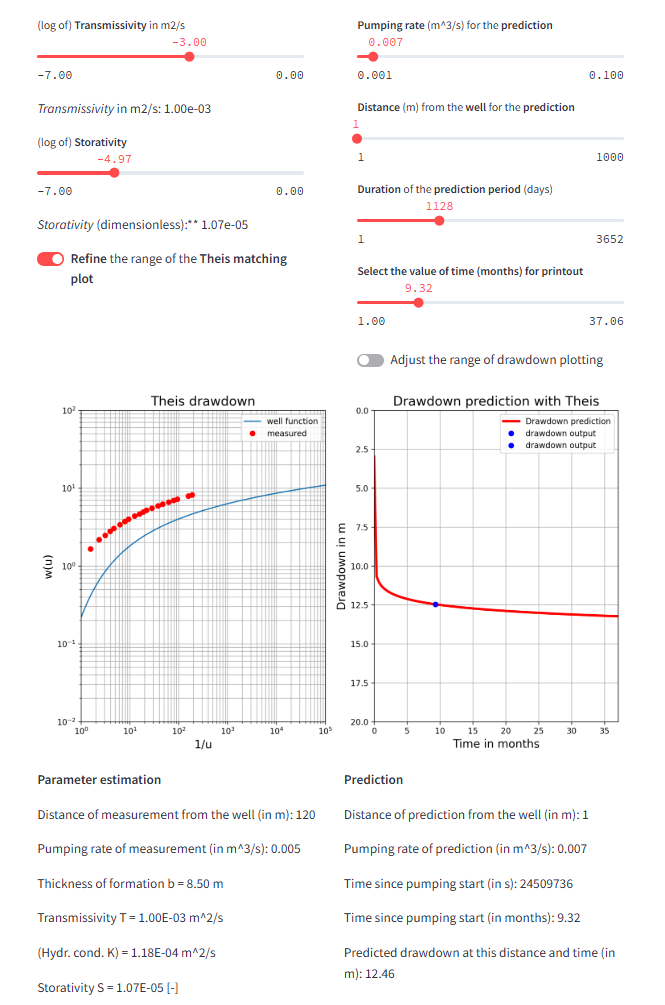
You can access the app here: https://theis-inverse-drawdown-random.streamlit.app/